PROGRAMMING AND DATA STRUCTURES - PRACTICAL WEEK 2
1). In the lecture on this topic we discussed the possible forms of different tiled square floors (in accordance to the size of the side of the square) and came up with three simple expressions for possible side sizes. (Click here to see the lecture notes on the tiler's problem.)
The possible side sizes that can make a square floor with L - shaped tiles that cover three squares and a single 1 by 1 tile are:
- Sides of the form 2^n (even numbers only)
- Sides of the form 3k+5 (a square of side of form 3k+1 surrounded by a border of thickness 2 units)
- Sides of the form 5x2^n
The 3 x 3 grid has side of neither of these forms (as n and k must be positive integers), therefore cannot be constructed.
i.e.
if 2^n = 3 then n = log3/log2 which isn't a positve integer.
if 3k+5 = 3 then k = -0.6666... which isn't a positive integer.
if 5x(2^n) = 3 then n = log(3/5)/log2 which isn't a positive integer.
When trying to construct the 3 x 3 sqaure there are only four possible ways of arranging the L - shaped tiles, e.g.
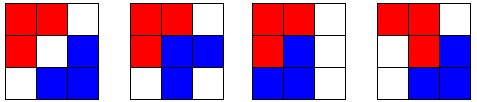
Blank coloured squares represent uncovered floor.
As you can see from all four arrangements, there are more than just one single sqaure left and none of the empty squares left are postioned to fit any more L - shaped tiles. From these diagrams and the calculations above it is clear that a 3 x 3 square floor cannot be tiled with unbroken L - shaped tiles which each cover three squares.
2). Is it possible to tile a 9 by 9 room with the usual rules? - well, to answer this question we siply have to fit the number nine to the three expressions for the lengths of side of the square floors that can be tiled.
if 2^n = 9 then n = 2log3/log2 which isn't a positive integer.
if 3k+5 = 9 then n=1.3333... which isn't a positive integer.
if 5x(2^n) = 9 then n = log(9/5)/log2 which isn't a positive integer.
A 9 by 9 square can be construcet however, but not with teh usual rules. I worked on the idea of having a border of thickness 2 round a 5 by 5 square, except the 5 by 5 square is not a perfect square, it has 2 L-shaped tiles that stick out, one from the corner, and one from one of the sides. The diagram below shows the 9 by 9 tiled floor.

L-shaped tiles are represented by the different colours.
As you can see, there is no need to use a sinle, 1 by 1 tile.
3). It is possible to tile a 14 by 14 floor. This can be done by putting four 7 by 7 tiled floors together to form a square. The way I tiled the 14 by 14 floor was quite similar to the way of tiling a floor with side of the form 2^n. I was able to tile a 7 by 7 square, leaving one of the squares in the grid uncovered. I then arranged four of these type floors, so a 2 by 2 square was left in the middle of them. This gap could then easily be filed using one L-shaped tile and one 1 by 1 tile.

L-shaped tiles are represented by different colours.
4). A 13 by 13 square can be construcetd by placing a border of thickness 3 around a 7 by 7 square. This is shown in the diagram below.

L-shaped tiles are represented by different colours.
The circumastance under which a 3 thickness 3 border can be added is when the side of the floor to be tiled is of the form 3k+1 (where k>1). The inside square will also have side of this form, but the side will be 3(k-2)+1 in length. e.g. for k=2 (a 7 by 7 floor)

.
5).
- Construction Of A 32 by 32 Tiled Floor:
The size of the side, 32, is of the form 2^n, i.e. 2^5 = 32. Four 16 by 16 squares (with a corner square missing) would be placed to leave a 2 by 2 gap, filled by one L-shaped tile and a single 1 by 1 tile.
- Construction Of A 17 by 17 Tiled Floor:
The size of the side, 17, is of the form 3k+5, i.e. (3x4)+5=17. Here a boredr thickness 2 would surround a 13 by 13 square.
- Construction Of A 15 by 15 Tiled Floor:
To construct this floor I simply surrounded a 9 by 9 floor with as many 2 by 3 rectangles as I could. A 2 by 3 rectangle is made simply by putting 2 L-shaped tiles together. These rectangles are very useful as building blocks to tile odd number side floors. In the diagram below a 9 by 9 floor is surrounded with 48 2 by 3 rectangles.

L-shaped tiles are represented by the different colours.
- Construction Of A 22 by 22 Tiled Floor:
To construct this floor I will use four 11 by 11 squares each with a single square missing, to leave a gap of 2 by 2 in the middle, which can be filled by an L-shaped tile and a single 1 by 1 tile. I know I can make an 11 by 11 square with a single square missing because (11^2)-1 = 120, which is divisible by 6 meaning 2 by 3 rectangles can be used to construct it.
6). To tile any square room whose side length is an odd number you us ethe borderring techniques on any square larger than 7 by 7 (except for the 9 by 9 square). The borders you can use are thickness 2, thickness 3 or a border using 2 by 3 rectangles, depending on the size of the square. If the square of the length of the floor is divisible by 6, then all you need are 2 by 3 rectangles. For a square of length n, if (n^2)-1 is divisible by 6, then all you need are 2 by 3 rectangles and a single 1 by 1 square. In general
- If length of side is of the form 3k+1, use a thickness 3 border surrounding a square of length 3(k-2)+1.
- If length of side is of teh form 3k+5, use a thickness 2 border surrounding a square of length 3K+1.
- If length of side n, if n^2 is divisible by 6, use 2 by 3 rectangles.
- If length of side n, if (n^2)-1 is divisible by 6, use 2 by 3 rectangles and a single 1 by 1 square.
By Jaime-Ramon CASSAR.






