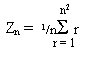
Using Magic Squares to Find Lines In Grids
OVERVIEW:
A magic square is a number grid where the squares in the grid are assigned specific numbers such that all lines and diagonals in the grid add up to the same number. After investigations of different sized grids, I came to the conclusion that a magic square of side n can only be used to identify lines and diagonals in the grid if n numbers in the grid add up to the same number 2n + 2 times.
EXPLANATION:
The 3 by 3 magic square can be used to identify lines and diagonals on the grid because the number of ways three numbers add up to the same number is equal to the number of lines and diagonals on the grid.
Finding the magic number: By logical reasoning you would want the magic number (the number all numbers on the same line or diagonal add up to) to be the number that is most commonly produced when adding any combination of n numbers from the n2 that are on the grid. This is found by working out the average sum of a combination of n numbers from n2 numbers.
Thus, the magic number (Zn) is given by the formula: (fig 1)
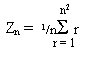
So for a 3 by 3 magic square the magic number is 1/3 *(1+2+3+4+5+6+7+8+9+10) = 15
The number of ways three numbers from 1 Ė 9 add up to 15 are:
1). 1+5+9 = 15
2). 1+6+8 = 15
3). 2+5+8 = 15
4). 2+6+1 = 15
5). 2+4+9 = 15
6). 3+4+8 = 15
7). 3+7+5 = 15
8). 4+5+6 = 15
Looking at the eight ways of adding up 3 numbers between 1 and 9 to produce 15, we can easily construct the 3 by 3 magic square. The number 5 is the number repeated only four times so it must be in the centre of the grid. The numbers 2,4,6 and 8 are repeated three times so they must be on the corners of the grid. 4,5 and 6 add up to give 15 so 4 and 6 must be opposite corners meaning 2 and 8 are also opposite corners. With this information we can construct the 3 by 3 magic square.
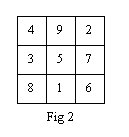
This magic square can be used to identify lines and diagonals on the number grid because the number of ways 3 numbers between 1 Ė 9 add up to produce the magic number is equal to the number of lines and diagonals. If there were more ways of producing the magic number than there are lines and diagonals then this technique could not be used to identify lines and diagonals on the grid.
If n numbers between 1 Ė n2 could be added to produce the same total more than 2n + 2 times (2n + 2 is the formula for the numbers of lines and diagonals.) the magic square could not be used. This is because some of the combinations of n numbers, adding up to produce the magic number would not be on either a line or a diagonal. So, using this total to identify a line or diagonal would be incorrect.
The Conditions For The n by n Magic Square to Be Used To Identify Lines:
If the number of ways n numbers between 1-n2 can be added to produce Zn is less than 2n + 2 a magic square cannot be constructed. This is because there wont be enough combinations to fit all the lines and diagonals. If the number of ways n numbers between 1-n2 can be added to produce Zn is greater than 2n + 2 a magic square will be useless. This is because there will be some combinations of n numbers that can be added to produce Zn that are not on either a line or a diagonal.
A 2 by 2 magic square is impossible. This can be seen by inspection of the sum of the combinations of any two numbers between 1 Ė 4.
1). 1+2 = 3
2). 1+3 = 4
3). 1+4 = 5
4). 2+3 = 5
5). 2+4 = 6
6). 3+4 = 7
Out of the 6 combinations of adding two numbers between 1 Ė 4 only the total of 5 is repeated, but it is repeated fewer times than the number of lines and diagonals so a magic square cannot be constructed.
The number 5 is repeated the most because it is the magic number Z2.
A 4 by 4 magic square can be constructed. The magic number Z4 for a 4 by 4 magic square is
ľ(1+2+Ö+15+16) = 34
To construct a 4 by 4 magic square I have chosen an easier method than writing out all the possible combinations of 4 numbers between 1 Ė 16 adding up to give 34. I will write down an ordered 4 by 4 number grid and swap around pairs of high numbers and low numbers to make sure that a pair of high numbers is paired up with a pair of low numbers on every line. I will swap the pairs in such a way to make all the lines add up to 34.
As you can see both diagonals add up to 34 already. If I swap the opposite centre edge pairs all the edges will also add up to 34. This is because I have swapped the smaller low number pairs with the larger high number pairs and the moderately sized low number pair with the moderately sized high number pair. In doing this I have compensated across the grid. (see Fig 4)
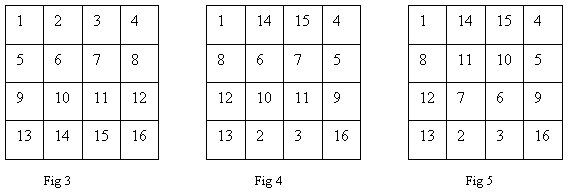
Looking at Fig 4 it is only the two central vertical lines and two central horizontal lines that donít quite add up to 34. Using the same swapping technique to compensate across the grid and keeping the diagonals the same it is possible to finish the construction of the 4 by 4 magic squares. By simply swapping the inside opposite diagonals I will ensure that all central vertical and central horizontal lines have a pair of high numbers with a pair of low numbers and thus making all lines and diagonals add up to 34. (see Fig 5). The magic square can be constructed but cannot be used to identify lines and diagonals because there are combinations of four numbers that arenít in a line that add up to Z4 (34).
E.g. 6,7,10,11. These numbers add up to 34, but arenít in a line or diagonal.
If some more conditions were introduced, then it would be possible to use the 4 by 4 magic square to identify lines and diagonals. E.g.
These arenít all the conditions youíd need to invalidate all combinations of numbers adding up to 34, that arenít on lines are diagonals. Introducing such conditions would make identification tedious. Assigning a co ordinate system to the grid that could identify lines and diagonals by seeing if the squares fit the available line equations would be the alternative.
Jaime - Ramón CASSAR